Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. It is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann-Landau notation or asymptotic notation.
Academics use big O, big Θ (theta), big Ω (omega) to describe runtimes.
O (big O)
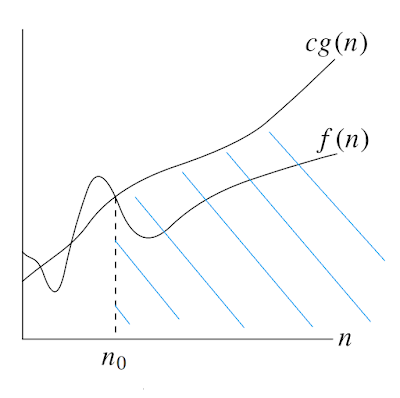 |
| f(n) = O(g(n)) |
O-notation gives an upper bound for a function to within a constant factor. We write f (n) = O(g(n)) if there are positive constants n0 and c such that to the right of n0, the value of f (n) always lies on or below cg(n).
Ω (big omega)
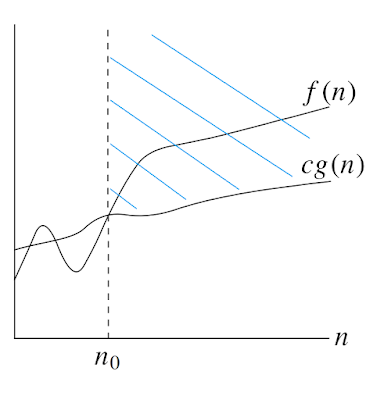 |
| f(n) = Ω(g(n)) |
Ω -notation gives a lower bound for a function to within a constant factor. We write f (n) = Ω (g(n)) if there are positive constants n0 and c such that to the right of n0, the value of f(n) always lies on or above cg(n).
Θ (big theta)
 |
| f(n) = Θ(g(n)) |
Θ-notation bounds a function to
within constant factors. We write f(n) = Θ(g(n)) if there exist positive constants n0, c1, and c2 such
that to the right of n0, the value of f(n) always lies between c1g(n) and c2g(n) inclusive.
Big O notation in software development industry
In software development industry, people seem to have merge all this concept into one. In software development we use Big O notation to work out how long an algorithm will take to run. This lets us understand how a piece of code will scale. It measures algorithmic efficiency.
Using O-notation, we can often describe the running time of an algorithm
merely by inspecting the algorithm’s overall structure. For example, the doubly
nested loop structure yields an O(n^2) on the worst-case running time.
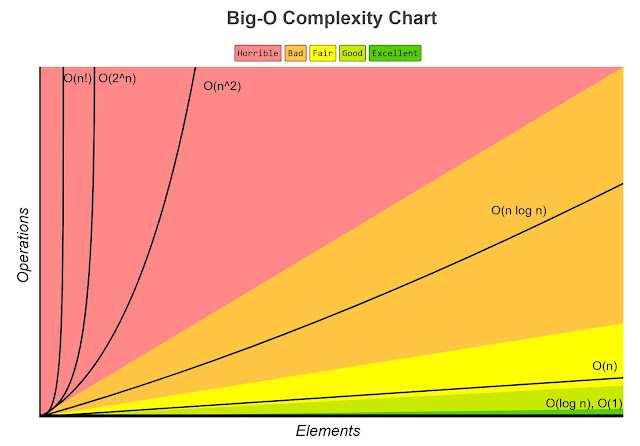
Running time of an algorithm
- O(log n)
- O(1)
- O(n)
- O(n log n)
- O(n^2)
- O(2^n)
- O(n!)